 |
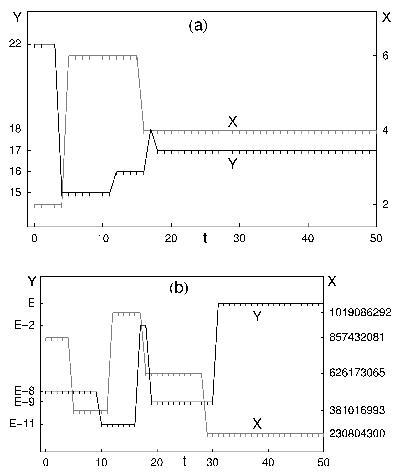 |
Cicadas of the genus Magicicada appear every 7, 13 or 17 years. The
fact that these are prime numbers has been regarded as a coincidence. We
developed a model with predators (X) and prey (Y) including mutations and
selection. We showed that prey (cicadas) with prime cycles are selected
(see example a) below) in order to optimally escape predators.
Changing our intentions from biological to number-theoretical, we set
arbitrarily large initial conditions and could thus use this model as a
generator for very large prime numbers (for example, in the figure b) below,
the Euler-prime E is selected).
 |
 |
Reports in our work:
in german:
![]() Der Spiegel Nr. 32, S. 148, 06.08.2001
Der Spiegel Nr. 32, S. 148, 06.08.2001
Presse-Information, Max-Planck-Gesellschaft.
Münchener Merkur, 4./5.05.2002
Sonntagszeitung, Zürich, 5.05.2002
Berliner Morgenpost, 18.07.2004
Publications on the cicada model:
M. Markus, "A Biological Generator of Prime Numbers", Max-Planck Research 2, 4-5 (2002)
M. Markus and E. Goles, "Cicadas showing up after a prime number of years", Math. Intelligencer 24, 30-33 (2002)
M. Markus, O. Schulz and E. Goles, "Prey population cycles are stable in an evolutionary model if and only if their periods are primes", Science Asia 28, 199-203 (2002)
E. Goles, O. Schulz and M. Markus, "Prime number selection of cycles in a predator-prey model", Complexity 6, 33-38 (2001)
E. Goles, O. Schulz and M. Markus, "A biological generator of prime numbers", Nonlinear Phenom. in Compl. Syst. 3, 208-213 (2000). In the web.
E. Goles, O. Schulz and M. Markus, "Prime number selection of cycles in a predator-prey model", Complexity 6, 33-38 (2001)
M. Markus, O. Schulz and E. Goles, "Prey population cycles are stable in an evolutionary model if and only if their periods are primes", Science Asia 28, 199-203 (2002)
M. Markus, "A Biological Generator of Prime Numbers", Max-Planck Research 2, 4-5 (2002)
M. Markus and E. Goles, "Cicadas showing up after a prime number of years", Mathematical Intelligencer 24, 30-33 (2002)
142. M. Markus, O. Schulz and E. Goles: Comment on "Emergence of Prime Numbers as the Result of Evolutionary Strategy". Physical Review Letters 95, 229891 (2005).
Other publications on population dynamics:
M. Markus, "Are 1D-Maps of Any Practical Use in Ecology?" Ecological Modelling 63 (1992), pp. 243-259
J. Roessler, M. Kiwi and M. Markus, "Ecosystems under varying ambiental conditions" in: 'From Chemical to Biological Organization' (ed. by M. Markus, S. Muller and G. Nicolis), Springer-Verlag, Berlin, pp. 319-330 (1987)
M. Markus, B. Hess, J. Roessler and M. Kiwi, "Populations under periodically and randomly varying growth conditions", in: 'Chaos in Biological Systems' (ed. by H. Degn, A. Holden and L.F. Olsen) Plenum Press, N.Y. (1987) pp. 267-277