Typical intermingled basins (black and white points, corresponding to
different initial conditions, lead to different oscillations):
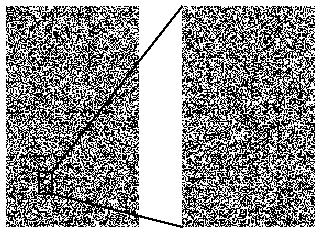
If a system displays two modes of behaviour for the same set of control
parameters, then the set A (in phase space) leading to one mode is said
to be riddled with respect to the set B leading to the other mode, if every
neighbourhood of every point in A contains points in B.
If A is riddled with respect to B and B is riddled with respect to A, then A and B are said to be intermingled. This means that conditions leading to the two modes are so close to each other as rational and irrational numbers. (See figure below, in which black and white points lead to different modes). It also means that improvements in calculational or experimental accuracy of initial conditions are not of much help in predicting the outcome.
We found riddled or intermingled basins in: i) the oscillatory Belousov-Zhabotinsky
(BZ) reaction; ii) a mechanical device consisting of coupled elastic arches.
Furthermore, we found an apparent riddling for (unavoidable) finite accuracy
in a periodically tilting box with a few particles. In addition, we found
that transient riddling has been overlooked so far in the logistic equation,
and appears also in the BZ reaction.
Typical intermingled basins (black and white points, corresponding to
different initial conditions, lead to different oscillations):
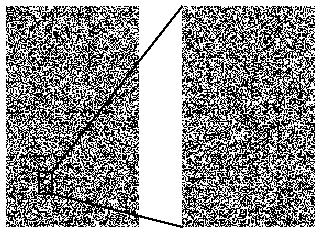
Publications:
M. Woltering and M. Markus, "Riddled-like basins of transient chaos", Phys. Rev. Lett. 84(4), 630-633 (2000)
M. Woltering and M. Markus, "Riddled basins of the Belousov-Zhabotinsky reaction", Chem. Phys. Lett. 321 (5-6), 473-478 (2000)
M. Schmick, E. Goles and M. Markus, "Intermingled basins due to finite accuracy", Phys. Rev. E 62, 397-401 (2000)
M. Woltering and M. Markus, "Riddled basins of coupled elastic arches",
Phys. Lett. A 260, 453-461 (1999)
![]()
![]()