CELLULAR AUTOMATA

Cellular automata (CA) are descriptions of dynamic phenomena that do not use equations but rules, like in a game. Thus, CA can describe nature in a "linguistic" way. They are usually fast and easy to programm. Furthermore, the computing time is, in general, lower than using partial differential equations.

CA are descriptions of phenomena that are discrete in time, in space and in states. The state of a spatial cell at a given time step is determined by the states in a neighbourhood of that cell at the previous time step, according to the rules.

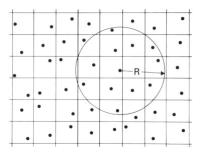
A drawback in CA has been that the shape of the simulated spatial structures depends on the shape of the cells. To avoid this, we used a quasi-stochastic spatial discretization (shown below; circular neighbourhood with radius R). Such a CA renders isotropy (i.e. "round" structures) and can thus be used for quantitative analyses that require well-defined curvatures, e.g. the eikonal relationship.

The simulation example shown below is that of depolarizing waves in the heart (t=12). They emerge from the sinus node (point at t=0) and they break at a region of transitory lower repolarization rate (rectangle; t=0). Such a region may appear in scars after an infarct. After breaking, the two free wave ends curl into spirals. These spirals are much faster than the normal waves. This causes an abnormally fast heart beat (tachycardia), which is usually medicated by a total heart depolarization that permits the sinus node to reassume its function.

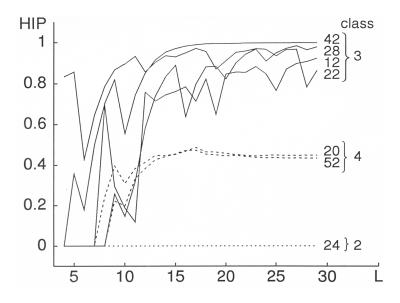
In general, CA can lead to four different modes: i) homogeneity ("class 1"); ii) periodicity ("class 2"); iii) chaos ("class 3"); and iv) an erratic alternation of periodicity and chaos ("class 4"). The latter has been called "edge of chaos" and is believed to play an essential role in biological systems accounting both for their flexibility and their reliability. We developed a simple way of quantifying this classification: we consider CA with an extremely low number of cells, consider all possible initial conditions, and quantify by the number of final modes with periods larger than 1, divided by the total number of modes ("high periods": HIP, plotted below for a one-dimensional example, against the CA length L).
 
 
 

Quasi-stochastic discretization:

Simulation of tachycardia in heart muscle:

 

Publications:

M. Markus, M. Schmick and E. Goles: "Hierarchy of Cellular Automata In Relation To Control Of Chaos Or Anticontrol. In: Complexus Mundi Emergent Patterns in Nature". (Ed.) M. M. Novak, World Scientific, New Jersey, 2006, 297-304

M. Markus, M. Schmick and E. Goles: "Tracks Emerging by Forcing Langton's Ant with Binary Sequences". Complexity 11 27-32 (2006)

A. Greilich, M. Markus and E. Goles: "Control of spatiotemporal chaos: dependence of the minimum pinning distance on the spatial measure entropy". European Physical Journal D 33, 279-283 (2005)

D. Fischer, E. Goles and M. Markus: "Frieze-Generation Using Artificial Life". In: Isama-Bridges. (Ed. by J. Barrallo, N. Friedman, R. Sarhangi, C. Séquin, J. Martínez and J.A. Maldonado), 151-160, University of Granada (2003)

M. Markus and B. Hess, "Isotropic cellular automaton for modelling excitable media", Nature 347, 56-58 (1990)

M. Markus, D. Boehm and M. Schmick, "Simulations of vessel morphogenesis using cellular automata", Mathematical Biosciences 156, 191-206 (1999)

M. Markus, A. Czajka, D. Boehm, T. Hahn, T. Schulte and A. Ribeiro, Phenomenology of Cellular Automata Simulations of Natural Processes, in: Cellular Automata and Complex System (ed. by E. Goles & S. Martinez), Kluwer, Dordrecht, pp. 23-47 (1999)

M. Markus, T. Schulte and A. Czajka, "Disordered waves in an excitable medium consisting of two layers: catalytic gel and non-catalytic solution", Physical Review E 56, 1-4 (1997)

M. Markus, T. Hahn and I. Kusch, "A novel quantification of cellular automata", J. Parallel Comp. 23, 1635-1642 (1997)

M. Markus, I. Kusch, A. Ribeiro and P. Almeida, "Class 4 cellular automata simulating diverse physical systems", Int. J. Bifurcation & Chaos 6, 1817-1827 (1996)

I. Kusch and M. Markus, "Mollusc shell pigmentation: cellular automaton simulations and evidence for undecidability", Journal of theoretical Biology 178, 333-340 (1996)

M. Markus and I. Kusch, "Cellular automata for modelling the shell pigmentation of molluscs", Journal of Biological Systems 3, 999-1011 (1995)

M. Markus and K. Stavridis, "Wavefront deformations in excitable media: chemical lenses and ripples", Phil. Trans. Roy. Soc. A 347 (1994), pp. 601-605

H. Schepers and M. Markus, "Two Types of Performance of an Isotropic Cellular Automaton: Stationary (Turing) Patterns and Spiral Waves", Physica A 188 (1992), pp. 337-343

M. Markus, Zs. Nagy-Ungvarai and B. Hess, "Phototaxis of spiral waves", Science 257, (1992), pp. 225-227

M. Markus, "Modelling morphogenetic processes in excitable tissues using novel cellular automata". Biomed. Biochim. Acta 49, 681-696 (1990)