|
|
configurrations: |
|
 |
 |
 |
Granular media, such as sand or industrial granulates, display properties
that are not common to those of liquids or those of solids. We investigate
such media, looking at their properties in the limit of extremely few (less
than 40) particles.
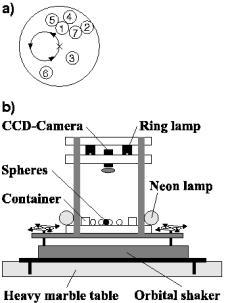
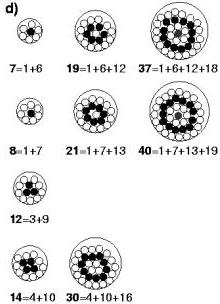
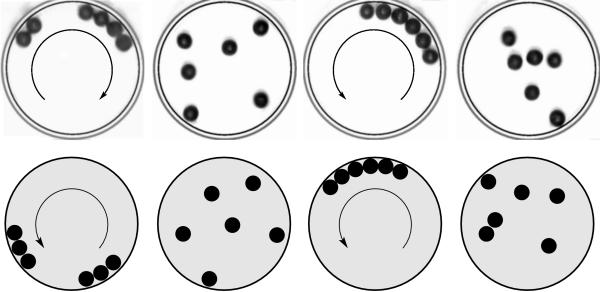
The system shown below consists of N spheres in a dish. They are swirled horizontally and periodically, so that the center of the dish describes a circle (a). Only certain numbers ("magic numbers") of spheres organize into rings (d). This occurs within a wide range of swirling frequencies, swirling amplitudes, or dish sizes.
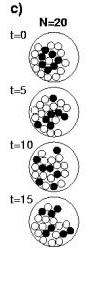
Taking out a sphere from N=21 causes chaotic mixing (c). Putting back
the sphere causes reorganization into rings; putting in another sphere
(N=22) yields again chaotic mixing.
|
|
configurrations: |
|
 |
 |
 |
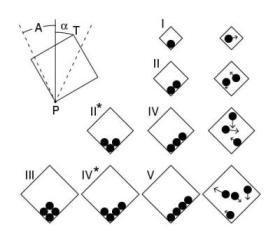
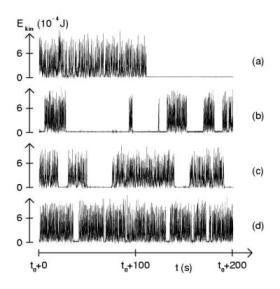
The periodically tilted box shown below shows an intermittent route
to chaos, on increasing the tilting amplitude or frequency. In other words,
the system can display erratic transitions between a solid-like and a gas-like
state. Shown below is the on-off behaviour of granular temperature.
|
|
|
 |
 |
Experiments with spheres containing magnetic dipoles and exposed to a periodical magnetic field were performed. Sketch of the setup:
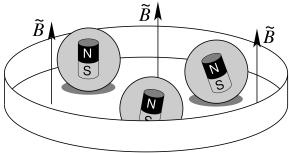
We observed intermittent behaviour. The following figure shows experiments (upper row) and simulations (lower row) at times: 55s, 75s, 130s and 145s (columns):
Reports on our work:
De Volkskrant, 4. 12. 1999, p. 3W
Publications:
S. Viridi, P. Grete and M. Markus, "A minimal mechanical device displaying bona fide resonance", Physics Letters A 372, 1040-1043 (2008)
M. Schmick and M. Markus, "Gaussian Distribution if rotational velocities in a granular medium", Physical Review E78, 010302 (2008)
O. Schulz and M. Markus, "Velocity distributions of camphor particle ensembles", Journal of Physical Chemistry B 111, 8175-8178 (2007)
M. Schmick, Q. Liu, Q. Ouyang, M. Markus, "Fluctuation theorem for a single particle in a moving billiard: Experiments and simulations", Physical Review E 76, 021115 (2007)
S. Viridi, M. Schmick and M. Markus, "Experimental observations of oscillations and segregation in a binary granular mixture", Physical Review E 74, 041301 (2006)
S. Viridi, M. Schmick and M. Markus, " 'Granular Clock' and Full Segregation in a Shaken, Binary Granular Medium: Experiments and Simulations", Nonlinear Phenomena in Complex Systems 9, 352-359 (2006)
M. Markus and M. Schmick, "Intermittency in connected hamiltonian systems". Physica A 328, 335-340 (2003).
M. Schmick and M. Markus, "Evidence for intermittency in a granular medium: experiments and simulations". Discrete Mathematics and Theoretical Computer Science AB, 1-10 (2003). In the web.
M. Schmick, E. Goles and M. Markus, "On-off intermittency and intermingledlike basins in a granular medium", Phys. Rev. E 66, 066214/1-4 (2002).
M. Markus, K.Koetter, M. Schmick, M. Grewe and E. Goles, "Selforganization of interacting, round particles into symmetric or asymmetric aggregates", in: 'Symmetry 2000' (I. Hargittai & T. Laurent, eds.), Portland Press, London, 377-348 (2002)
M. Schmick, E. Goles and M. Markus, "Intermingled basins due to finite accuracy", Phys. Rev. E 62, 397-401 (2000)
M. Scherer, K. Koetter, M. Markus, E. Goles and I. Rehberg, "Swirling granular solidlike clusters", Phys. Rev. E 61, 4069 (2000)
K. Koetter, E. Goles and M. Markus, "Shell structures with 'magic numbers' of spheres in a swirled dish", Phys. Rev. E 60, 7182-7185 (1999)
M. Markus, K.Koetter, M. Schmick, M. Grewe and E. Goles, "Self-organization
of interacting, round particles into symmetric or asymmetric aggregates"
in: 'Symmetry 2000' (I. Hargittai & T. Laurent, eds.), Portland Press,
London, in press
![]()
![]()